Solución adivinanzas

Os traemos las soluciones de las adivinanzas de la semana pasada. ¿Habrá sorpresas? Abre bien los ojos...

1. Los cuatro nueves.

9/9+99=100

2. A oscuras.

El hombre tendría que coger la mitad más uno para asegurarse de conseguir un par de un mismo color. Es decir, 11.

3. Una sencilla operación.

Es correcto si hablamos del tiempo. Es correcta hablando de horas: si sumamos tres horas a las once serán las dos.

4. El problema de las doce monedas.

En primer lugar distribuiremos las monedas en tres grupos de cuatro. Uno de ellos irá en cada brazo de la balanza y un tercero en la mesa. Si la balanza muestra un equilibrio, ello querrá decir que la moneda falsa con un peso diferente no está entre ellas sino entre las de la mesa. En caso contrario, estará en uno de los brazos.

En cualquier caso, en la segunda ocasión rotaremos las monedas en grupos de tres (dejando una de las originales fija en cada posición y rotando el resto). Si existe un cambio en la inclinación de la balanza, la moneda diferente está entre las que hemos rotado.

Si no hay diferencia, está entre las que no hemos movido. Retiramos las monedas sobre las que no hay duda que no son la falsa, con lo que en el tercer intento nos van a quedar tres monedas. En este caso bastará con pesar dos monedas, una en cada brazo de la balanza y la otra en la mesa. Si hay equilibrio la falsa será la que esté en la mesa, y en caso contrario y a partir de la información extraída en las anteriores ocasiones, podremos decir cual es.

5. La ventana cuadrada.

La ventana debe ser un rombo. Seguirá midiendo 1x1 metros, sin obstáculos y entraría la mitad de la luz.

6. Cadena de números.

Buscamos el número de 0 o círculos que hay en cada número. Por ejemplo, 8806 tiene seis. Entonces, el resultado de 2581 es 2.

¿Sorprendido? 

¡Esperamos que te haya gustado y hayas acertado muchas!

Tangram

¡Hola Pitabloguer!

Es fin de semana y tu cuerpo lo sabe.

Por esto hoy te traemos un juego que tal vez ya conozcas, el TANGRAM.

Este juego es sencillo. Siete figuras a modo de puzzle con las que puedes hacer infinidad de siluetas. ¡Imaginación al poder!

TANGRAM

Más allá de la calculadora

Sabemos que a veces resulta complicado y laborioso resolver algunas operaciones o trabajar con algunas ecuaciones, y por eso a menudo utilizamos las calculadoras.

Hoy os traemos una calculadora virtual que nos permite mucho más que realizar cálculos: WolframAlpha.

¿Que qué diferencia a WolframAlpha de una calculadora normal?

WolframAlpha  permite tanto calcular como obneter información de algo. De esta manera podemos desde resolver una simple resta o suma hasta lo que se te ocurra: simplificar ecuaciones, resolver ecuaciones, resolver sistemas de ecuaciones, dibujar ecuaciones de hasta tres variables...

Es una herramienta muy interesante para el 99,9% de la gente.

Buscando a Pi

Seguro que ya conoces el número Pi (π). Ese 3,14 que usamos para calcular perímetros de circunferencias y superficies de círculos. Pero Pi no es 3,14, es mucho más.

Pi es un númro irracional. Esto quiere decir que Pi no puede expresarse como una fracción ^m⁄_n, donde m y n son enteros  y n es diferente a cero. Es por esto por lo que el número Pi tiene infinitos decimales.

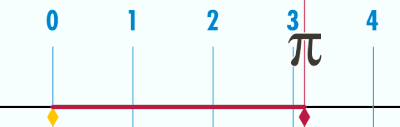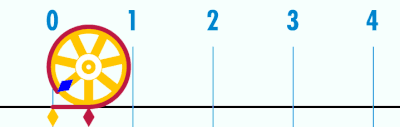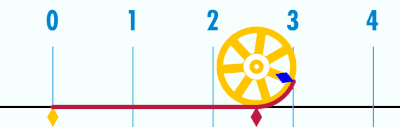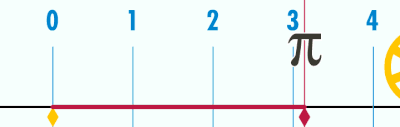
Pero ¿de dónde sale Pi? Pues Pi es la relación entre el perímetro (o longitud)  de de una circunferencia y su diámetro. Si tomamos una circunferencia de diámetro 1, su perímetro mide Pi.

Entonces ya sabemos cómo calcular el perímetro de una circunferencia conociendo su diámetro o su radio.

Perímetro = π · Diámetro = π · D = π · 2 · r = 2·π·r

¿Y cómo sabemos el área del círculo? Pues vamos a tratar de desmostrarte esa fórmula que ya conoces:

A = π · r²

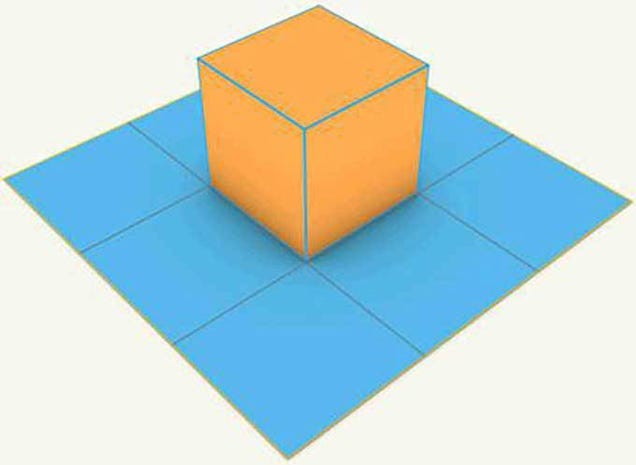
APROXIMACIÓN A CUADRADOS

Vamos a empezar dibujando un cuadrado que englobe el círculo.

Ahora vamos a calcular el área de este cuadrado.

Acuadrado = l · l = D · D = 2r · 2r = 4r²

Como este cuadrado es mayor que el círculo su área también lo es: π r² < 4r²

Ahora vamos a calcular el área del cuadrado inscrito en el círculo.  Esto vamos a hacerlo de dos formas distintas: como lo haría un listillo y como lo haría un bruto.

Método del listillo:

Un listillo rápidamente se daría cuenta de que el valor de la diagonal de este cuadrado es el diámetro del círculo. Entonces podemos usar el triangulo de Pitágoras para calcular los lados del cuadrado. 

D² = l² + l² = 2 · l²

l= √D²/2

Y por tanto el área de este cuadrado es:

Acuadrado = l · l = √D²/2 · √D²/2 = D²/2 = (2r)²/2  = 4r²/2 = 2r²

Método del bruto:

Un bruto dividiría el cuadrado en cuatro triángulos iguales y después crearía un rectángulo con estas cuatro piezas triangulares.

De esta manera llegaría de la misma forma a la ecuación del área:

Acuadrado = Arectángulo = b · h = 2r · r = 2 r²

Como este cuadrado es menor que el círculo su área también lo es: 2 r² < π r²

Así que con la aproximación a cuadrados hemos obtenido que: 2 r² < π r² < 4r²

APROXIMACIÓN A HEXÁGONOS

¿Quieres concretar un poco más el número π? Vamos a repetir el proceso pero con hexágonos en lugar de cuadrados.

Comenzamos inscribiendo el hexágono dentro del círculo.

Y como hemos visto que el Método del bruto es más cómodo de entender vamos a aplicarlo dividiendo el hexágono en seis triángulos equiláteros iguales.

Ahora movemos los triángulos de esta forma.

Por último calculamos el área del romboide resultante. ¿Recuerdas la fórmula del área del romboide? Si no es así, no te preocupes. Vamos a aplicar de nuevo el Método del bruto y... ¡un rectángulo!

¿Sabemos las medidas de este rectángulo?

Parece claro que su base es igual a tres veces el lado del triángulo, pero ¿y la altura?

Pues dividimos uno de los seis triángulos equiláteros en los que hemos dividido el hexágono inscrito trazando su altura (h) y obtenemos dos triángulos rectángulos iguales en los que podemos aplicar el triángulo de Pitágoras como hacía el listillo.

Si prestamos atención, nos damos cuenta de que conocemos el valor de la hipotenusa a, ya que se trata del radio del círculo y el valor del cateto menor b, ya que coincide con medio radio del círculo. Utilizamos el triangulo de Pitágoras y...

Por lo que ya conocemos la base del rectángulo (tres veces el lado del triángulo) y la altura, por lo que podemos calcular su área:

Como este hexágono es menor que el círculo su área también lo es: 

A su vez, como el hexágono se aproxima mejor al círuclo que el cuadrado, tenemos:

Ahora dibujamos el hexágono que inscribe al círculo.

Al dividir el hexágono en seis triángulos equiláteros iguales obtenemos unos triángulos de los que, a priori, solo conocemos que sus alguras, h, son iguales al radio, r. Por lo que esta vez resulta más complicado obtener las medidas de cada triángulo para poder calcular el área total del hexágono. Así que vamos a simplificar cálculos y vamos a optar por la Relación de Semejanza.

Conocemos que la altura, h, de uno de los seis triángulos equiláteros que compone el hexágono inscrito era 

y su base era el radio, r. Y conocemos que la altura, h, de uno de los seis triángulos equiláteros que compone el hexágono que inscribe es el radio, r. Así que aplicando la Relación de Semejanza podemos calcular la longitud de su base (llamamos B a la base de uno de los triángulos equiláteros que forman el hexágono que inscribe la circunferencia y A a la altura del mismo, llamamos b a la base de uno de los triángulos equiláteros que forman el hexágono inscrito en la circunferencia y a a la altura del mismo).

Con estos datos ya podemos calcular la superficie del romboide o rectángulo resultante.

Como este hexágono es mayor que el círculo su área también lo es: 

Así que a modo de resumen tenemos que:

O dicho de otra forma:

Este método de asemejar el círculo a polígonos de los que sí sabemos calcular el área nos permite ir acercándonos poco a poco al valor de Pi.

Al ser Pi un número irracional esto se podría repetir hasta el infinito. ¿Te animas a seguir?

Reforzando

¡Hola Pitáblogers!

Llevamos un tiempo sin recomendaros magníficos canales de YouTube sobre matemáticas. Os dejamos algunos en esta publicación.

STAND UP MATHS

En este canal un profesor de matemáticas juega, hace pruebas y experimentos matemáticos. El profesor es una mezcla entre profesor y cómico, le siguen más de 250 mil suscriptores. ¿Le conocemos?

VIDEO MATH TUTOR

Es una plataforma de apoyo para matemáticas con lecciones sobre temas específicos. ¡A por ello!

MATHADEMICS

Si quieres encontrar un canal con temas matemáticos muy prácticos e interesantes, no te lo pierdas.

PROFESOR 10 DE MATES

Un docente con miles de vídeos de matemáticas y física. Además, cuenta con su propio blog con el mismo nombre. ¡Muy recomendado!

MATEMOVIL

Este canal está dedicado sólo a los números. Muy a tener en cuenta si tienes dudas sobre algún tema concreto o te interesa algún truco matemático (que tiene muchos).

No te dejes ninguno por ver. ¡Te sorprenderán!

¿Serías capaz de calcular la altura de un edificio con una regla?

Vamos a empezar adaptando una curiosa historia.

<< Hace algún tiempo, recibimos la llamada de un colega profesor. Estaba a punto de ponerle un cero a un estudiante por la respuesta que había dado en un problema de física. Como el estudiante afirmaba que su respuesta era absolutamente acertada, acordaron pedir arbitraje de alguien imparcial y fuimos elegidos.

La pregunta del examen decía: "¿Qué harías para determinar la altura de un edificio con una regla?"

El estudiante había respondido: "Llevo la regla a la azotea del edificio y le ato una cuerda muy larga. Descuelgo la regla hasta la base del edificio, marco en la cuerda y después mido la longitud de la cuerda con la regla."

Realmente, el estudiante había planteado un serio problema con la resolución del ejercicio, porque había contestado a la pregunta, correcta y completamente. Por otro lado, si se le concedía la máxima puntuación, se estaría certificando su algo nivel de física. Pero la respuesta no confirmaba que el estudiante tuviera ese nivel.

Sugerimos que se le diera al alumno otra oportunidad. Le concedimos seis minutos para que me respondiera la misma pregunta. Pero esta vez con la advertencia de que en la respuesta debía demostrar sus conocimientos de física.

Habían pasado cinco minutos y el estudiante no había escrito nada. Le preguntamos si deseaba marcharse, pero me contestó que tenía muchas respuestas al problema. Su dificultad era elegir la mejor de todas. En el minuto que le quedaba escribió la siguiente respuesta:

"Cojo la regla y la tiro desde la azontea a la calle. Calculo el tiempo de la caída con un cronómetro. Después aplico la fórmula:

Altura = 0,5 G · T²

(donde G es la aceleración de la gravedad y T es el tiempo que acabo de calcular con el cronómetro). Y así obtengo la altura del edificio."

En este momento pedimos al estudiante que saliera del despacho. Le pusimos la nota más alta.

Tras salir del despacho, nos encontramos con el estudiante y le pedimos que me contara sus otras respuestas a la pregunta.

"Sí", contestó, "Este es un procedimiento muy básico para medir un edificio, pero también sirve. En este método, te situas en las escaleras del edificio en la planta baja. A medida que vas subiendo las escaleras, vas marcando con la regla y cuentas el número de marcas hasta la azotea. Multiplicas la longitud de la regla por el número de marcas que hiciste y ya tienes la altura. Este es un método muy directo."

"Perfecto", dijimos, "¿y de otra manera?"

"Probablemente, la mejor sea tomar la regla y golpear con ella la puerta del portero. Cuando abra, decirle: señor portero, aquí tengo una bonita regla. Si usted me dice la altura de este edificio, se la regalo."

En este momento de la conversación, le preguntamos si no conocía la respuesta convencional al problema.

Nos dijo que sí, que evidentemente la conocía. Pero que durante sus estudios, sus profesores habían intentado enseñarle a pensar. >>

Curioso, ¿No crees?

Pues ahora vamos a ver cuál es esa forma convencional de resolver el problema de calcular la altura de un edificio con una regla.

Lo primero que debemos hacer es buscar qué tienen en común el edificio y la regla, en qué son semejantes, y nos podría servir para saber la altura del edificio.

¿No se te ocurre? Pues aunque parezca raro, es ¡¡LA SOMBRA!! Sí, tanto el edifio como la regla dan sombra. Parece una tontería, pero fíjate qué curioso.

Si nos fijamos bien el edifio es alto y proyecta una gran sombra alargada, mientras que nuestra regla da una sombra mucho menor.

Como vemos en el dibujo, tanto el edificio y su sombra como la regla y su sombra forman triángulos. Pues estos triángulos, al tener sus ángulos iguales, son semejantes. ¿Y esto para qué sirve? Pues sencillo. Ya hemos visto que la sombra del edificio, B, es mayor que la sombra de la regla, b, porque el edificio, A, es mayor que la regla, a. Pero además la sombra del edificio, B, es tantas veces mayor que la sombra de la regla, b, como el edificio, A, es mayor que la regla, a.

Poniendo un ejemplo: Si la sombra del edificio, B, es 12 veces más grande la sombra de la regla, b,

B = 12 · b

entonces el edificio, A, será 12 veces más grande que la regla, a.

A = 12 · a

Si aplicamos un poco de las matemáticas que sabemos tenemos que: 

O expresado de otras maneras:

Sencillo, ¿verdad? Pues esto ocurre siempre que dos figuras, triángulos o no, son semejantes (sus ángulos son iguales, solo cambia su tamaño).

¿Encuentras otra forma de medir la altura de un edificio usando una regla?

Adivina adivinanza...

¿Qué tal estás Pitábloger? Tenemos unos acertijos que seguro te van a traer de cabeza. En una semana os dejaremos las soluciones en el blog.

1. Los cuatro nueves.

¿Cómo podemos hacer que cuatro nueves den como resultado cien?

2. A oscuras.

Un hombre se levanta por la noche y descubre que no hay luz en su habitación. Abre el cajón de los guantes, en el que hay diez guantes negros y diez azules. ¿Cuántos debe coger para asegurarse de que obtiene un par del mismo color?

3. Una sencilla operación.

¿En qué momento será correcta la operación 11+3=2?

4. El problema de las doce monedas.

Disponemos de una docena de monedas visualmente idénticas, de las cuales todas pesan lo mismo excepto una. No sabemos si pesa más o menos que las demás. ¿Cómo averiguaremos cual es con la ayuda de una balanza en como máximo tres oportunidades?

5. La ventana cuadrada.

Un noble tenía un salón con una sola ventana, cuadrada y de 1m de alto por 1m de ancho. El noble tenía un problema ocular, y la ventana dejaba entrar mucha luz. Llamó a un constructor y le pidió que alterara la ventana para que sólo entrara la mitad de la luz. Pero tenía que seguir siendo cuadrada y con las mismas dimensiones de 1x1 metros. Tampoco podía usar cortinas o personas o vidrios de color, ni nada semejante. ¿Cómo puede el constructor solucionar el problema?

6. Cadena de números.

¿Podrás resolver la última relación?

8806  => 6

7111  => 0

6666  => 4

1111  => 0

7662  => 2

9312  => 1

0000  => 4

2222  => 0

3333  => 0

5555  => 0

8193  => 3

8096  => 5

7777  => 0

9999  => 4

7756  => 1

6855  => 3

9881  => 5

5531  => 0

2581  => ¿?

Tienes una semana hasta que subamos las soluciones. ¿Podrás solucionar todas?

Desvelando el truco del Mago Pimágoras

¿Quieres saber cómo acierta el Mago Pimágoras tu carta?

¿Funcionará la poción de amor que me dio el mago Pimágoras?

Pues este truco tiene truco. Un truco matemático.

Si prestas atención el mago coloca las cartas formando tres columnas de nueve cartas cada columna. Veintisiete cartas en total. No te dice nada este número, ¿verdad?

¿Recuerdas como funciona el sistema binario? Pues el Mago Pimágoras usa el sistema ternario o sistema de base 3. En este sistema se emplean tres dígitos los dígitos 0, 1 y 2. Y si calculamos las potencias de base 3 tenemos:

Pues como el Mago Pimágoras ya sabía esto, lo ha usado asignando un número de base 3 a cada carta.

¿Cómo lo hace?

Pues el Mago Pimágoras cambia las cartas de columna cada vez que reparte. Así que, si asigna a la columna izquierda el 0, a la central el 1 y a la derecha el 2 (sistema cúbico o sistema de base 3) y reparte las cartas tres veces tenemos... 3³ = 27.

Esto quiere decir que la carta que tiene asignado el número 102 aparecería primero en la fila central (1), después en la fila izquierda (0) y por último en la derecha (2) cada una de las veces que el Mago Pimágoras reparte.

Sabemos que suena algo difícil de entender, pero te dejamos un vídeo explicativo por si quieres hacer este truco de magia a tus amig@s (en el vídeo hacen el truco con veintiuna cartas, pero se hace igual con veintisiete).

Poesía matemática. Uno y Cero

Si te decimos que las matemáticas son poesía, ¿qué nos dirías? Las matemáticas pueden servirte para mostrar tus sentimientos.

¿Te parece difícil? Te mostramos la magnífica poesía de César Brandon.

"Uno no quería contar con nadie, y Uno no entendía por qué era impar si antes de él había alguien.

Uno no quería contar con nadie, y Uno sentía que después de él estaba el infinito.

Y a Uno lo sempiterno le daba miedo, así que Uno, muerto de pavor, se fijó en Cero.

Y cuando Uno vio a Cero, pensó que cero era el número más bonito que había visto y que, aun viniendo antes que él, era entero.

Uno pensó que en Cero había encontrado el amor verdadero, que en Cero había encontrado a su par,

así que decidió ser sincero con Cero y decirle que aunque era un cero a la izquierda, sería el cero que le daría valor y sentido a su vida.

Eso de ser el primero ya no le iba, asi que debió hacer una gran bienvenida.

Juntos eran pura alegría y se completaban. Uno tenía cero tolerancia al alcohol, pero con Cero se podía tomar una cerveza cero por su aniversario, aunque para eso tuviesen que inventarse una fecha cero en el calendario.

Cero era algo cerrado y le costaba representar textos pero, junto a Uno, hacían el perfecto código binario.

Eran los dígitos del barrio y procesaban el amor a diario, pero uno no sabe lo que tiene hasta que lo pierde, así que Uno perdió a Cero.

Y para cuando Uno se dio cuenta, Cero ya contaba de la mano con Menos Uno, que a pesar de ser algo negativo le trataba como una reina.

A Cero le gustaba que Menos Uno fuera original, tener un hueco en Menos Uno, un guion con el que podían jugar.

Cero le gustaba que Menos Uno no fuese uno más, que Menos Uno no fuese ordinal.

Que fuese justamente competitivo y que cuando jugasen al UNO, Menos Uno no le dejase ganar.

Cero sentía que a diferencia de Uno, Menos Uno sí le trataba como un número de verdad.

Y Menos Uno no ponía peros, ni pretendía darle valor a cero poniendo comas entre ellos.

Menos Uno no tenía complejos, y cuando hacían el amor, a menos uno le encantaba estar bajo cero.

Y Uno, una vez más se volvió a quedar solo, separado como una unidad.

Sin Cero, su vida se consumía como una vela. Sin Cero, el tiempo en él hacía mella...

Y Uno empezó a contar pero sin Cero, se olvidó de los besos de Cero, del sexo con Cero, de los celos de Cero...

Y uno empezó a contar, pero sin Cero.

Uno se olvidó de Cero y le dijo adiós. Uno se olvidó de Cero y tal vez hasta del amor, y empezó a contar hasta lo que más miedo le daba: hasta el infinito.

... O tal vez solo hasta dos."

César Brandon.

F3L1Z S4N V4L3NT1N

¡Feliz San Valentín amante de las matemáticas!

Hay muchas formas de declarar el amor a nuestr@ amad@, pero los Pitablogers tenemos una muy especial de deciros cuanto os queremos:

9x - 7i > 3 (3x - 7u)

¿Qué? ¿Cómo? No te impacientes y trata de despejar la i.

¿Creías que hoy no iba a acordarme de ti?

Y recuerda:

" - odio + amor.

x toda la vida / tú y yo "

Solución al puzzle ruso

¿Encontraste la solución del puzzle ruso?

No te preocupes, por fin hoy vamos a desvelar la solución.

• Paso 1. 

• Paso 2.

• Paso 3.

• Paso 4.

• Paso 5. 

Sistema Binario 10 (segunda parte)

¿Viste la entrada que publicamos sobre el sistema binario? ¿Quieres saber más?

Hoy vamos a profundizar sobre este curioso sistema.

Todos sabemos contar: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12... Pero, ¿Cómo se cuenta en binario?

Si te fijas en el sistema decimal, el que usamos normalmente, comenzamos con las unidades 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9 y ¿qué ocurre cuando gastamos los diez dígitos de los que disponemos? Pues acompañamos a las unidades con las decenas: 10, 11, 12, 13...97, 98 y 99 ¿Y al completar todas estas combinaciones de dos dígitos? Pues añadimos la centena y así sucesivamente.

Pues el sistema binario es un sistema que se compone únicamente del 0 y el 1. Así que comenzamos contando por 0 y 1. ¿Y después? Pues añadimos otra cifra más para continuar la enumeración: 10 y 11 ¿Y ahora? Pues 100, 101, 110 y 111. ¿Lo vas siguiendo? ¿Serías capaz de continuar la enumeración?

¿Hay alguna forma de convertir un número binario en decimal? Pues hay una forma sencilla de hacerlo. Vamos a comparar la enumeración decimal y la binaria.

DECIMAL >> BINARIA

Si prestas un poco de atención te darás cuenta de en el sistema binario hay dos números solo con una cifra (0 y 1), otros dos números con dos cifras (10 y 11), cuatro con tres cifras (100, 101, 110 y 111) y ocho con cuatro cifras (dejamos que los veas tú). ¿Cuántos habrá de cinco cifras?

Pues fíjate, este sistema se llama binario porque solo usa dos cifras. Así que vamos a jugar con el número dos.

Curioso, ¿no crees?

Pues conocido esto ya estamos en disposición de convertir un número del sistema binario al sistema decimal. Pongamos por ejemplo el número 10111. El primer paso es ver qué cifras muestran el 1 y cuales el 0. Y ahora realizamos la siguiente operación según la posición de los 1 y los 0.

Y ahora, ¿te parece que el código binario es una pesadilla?